论文撷英｜《一种基于扩展平均场强化学习的非合作边界控制方法》

Li, X., Zhang, X., Qian, X., Zhao, C., Guo, Y., & Peeta, S. (2024). Beyond centralization: Non-cooperative perimeter control with extended mean-field reinforcement learning in urban road networks. Transportation Research Part B: Methodological, 186, 103016.

国际著名学术期刊《Transportation Research Part B: Methodological》2024年8月刊发表了我院学者的论文《一种基于扩展平均场强化学习的非合作边界控制方法》（Beyond centralization: Non-cooperative perimeter control with extended mean-field reinforcement learning in urban road networks）。李兴华教授为第一作者，博士生张昕源为第二作者，郭赟韬副教授为论文的通讯作者，论文的合作作者包括莱斯大学助理教授钱昕午、同济大学交通运输工程学院副教授赵聪及佐治亚理工教授Srinivas Peeta 。

文章摘要：边界控制类管理措施能够通过调节进入城市区域路网的交通流量来调控路网的运行状态。当前基于宏观基本图（Macroscopic Fundamental Diagram，MFD）的边界控制方法在实际应用中面临挑战，因为它难以为每一条进入区域的入境道路单独设定控制流率，存在一定的局限性。为此，有研究提出了基于细胞传输模型（Cell Transmission Model，CTM）的边界控制方法。这类方法虽然有效地解决了为特定道路单独设置流率的问题，但其隐含的中心化假设条件要求区域内存在一个理想的管理主体，能够控制路网内所有交通需求产生点的流率。在实际场景中，更切合实际的设定是区域中存在两类不同的交通需求产生点：一类是跨越区域边界入境的道路，另一类是区域内部的交通需求产生点（如停车场）。这两类主体间可能缺乏必要的物理连接或沟通协议来实施协同控制策略，更重要的是，它们代表不同的利益相关者。这些利益相关者拥有不同的控制目标、决策和行动，同时各主体之间又会相互影响。为了避免陷入对所有利益相关者都不利的“双输”局面，本研究提出了一种基于离散控制框架的非合作博弈模型，以及与之配套的拓展平均场论多智能体强化学习算法（Extended Mean-Field Reinforcement Learning，EMFRL），用于寻找纳什均衡点。实验结果表明，在不增加额外成本的情况下，本研究提出的EMFRL算法能够使这两类主体在离散框架下实现与中心化控制相近的表现。

关键词：边界控制、宏观基本图、细胞传输模型、离散控制框架、平均场近似、多智能体强化学习

论文链接：

https://kwnsfk27.r.eu-west-1.awstrack.me/L0/https:%2F%2Fauthors.elsevier.com%2Fa%2F1jMNXhVEBCe9v/1/01020190733ad315-1aa4f366-3c46-413a-9bd8-a835dd7df811-000000/UAbgagkWxgsL-ddzXiEmMt9WMQc=380

研究贡献

- 本研究采用非合作博弈框架来解释边界控制问题中不同利益相关者之间的交互关系

- 将宏观基本图概念引入平均场论，提出了一种兼容异构智能体的扩展平均场理论

- 提出了扩展平均场强化学习算法，并对该算法的近似性与收敛性进行了证明

- 为克服平均场强化学习中存在的“鸡生蛋蛋生鸡”问题，本研究还提出了一种平均场动作预测器，有效解决了这一难题

研究背景

宏观基本图（MFD）描述了路网流量与密度或累积量与完成量之间的关系，是评价路网运行状态的重要指标。基于准确定义的MFD，边界控制能有效优化路网交通状态。然而，获取MFD并非易事，且MFD会随路网动态管控措施的变化而变化。此外，基于MFD的边界控制方法无法为每条边界道路设置单独的控制等级，这限制了其应用场景。

针对这一问题，有研究采用基于细胞传输模型（CTM）的边界控制方法，通过混合整数线性规划（MILP）为每条边界道路设置单独的控制等级。但这种方法假设存在一个掌握所有流量控制信息的中央管理者，在实际应用中可能遇到困难。

为应对这些挑战，研究提出了一种分布、非合作的多主体城市边界控制博弈框架。该框架包含边界主体和若干个内部主体，它们有着相互独立的决策目标、信息输入和控制策略。研究旨在寻找构成纳什均衡的策略集合，并提出了一种新颖的多智能体强化学习框架，结合平均场论解决该博弈中大规模智能体协调训练的难题。该方法符合“分布学习、分布执行”范式，可有效避免多主体城市边界控制问题中的协调难题，并减少主体间的通讯开销。相比既有方法，该研究在策略求解时间和支持多主体共同决策方面具有优越性。

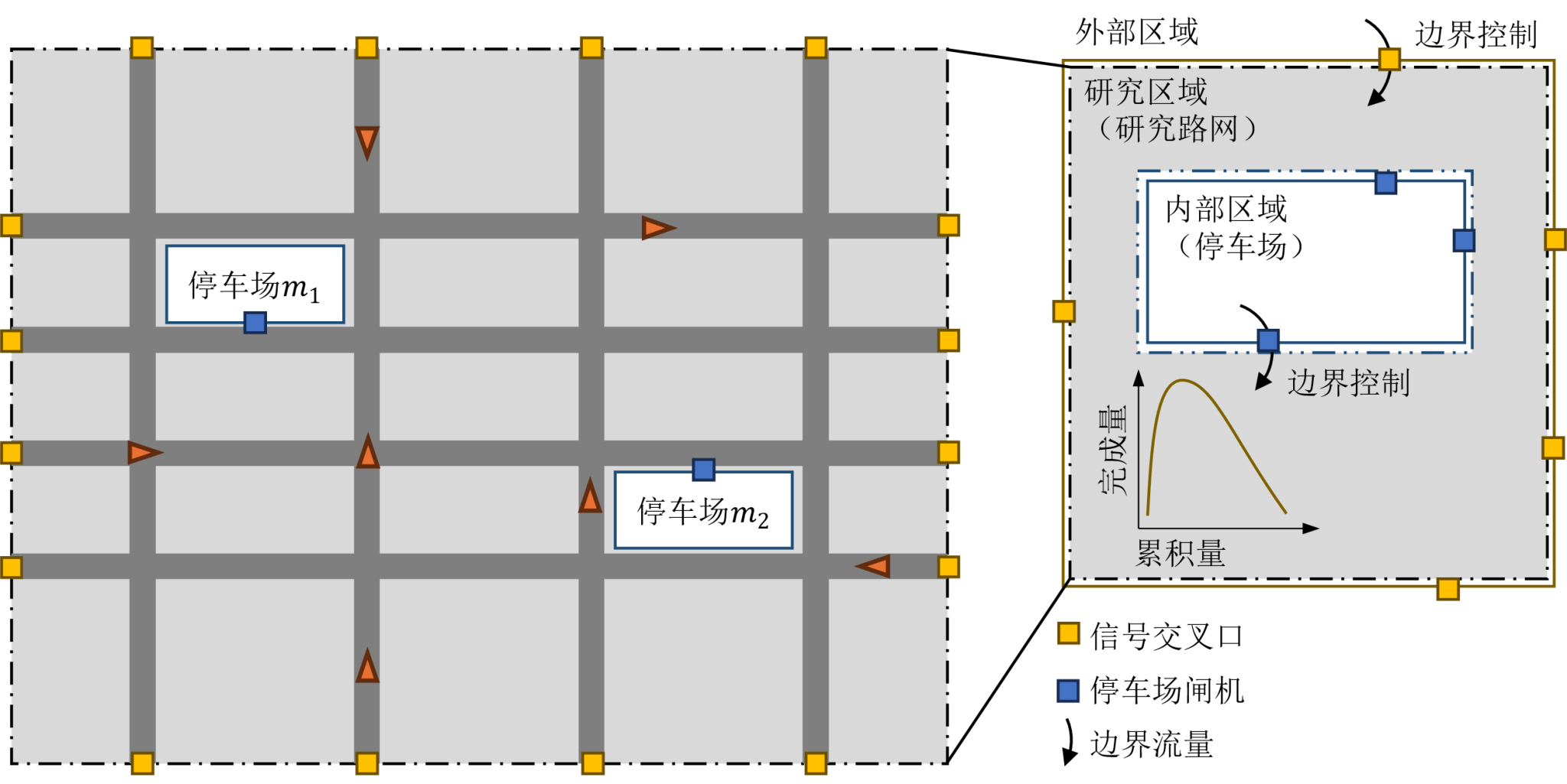
多主体城市边界控制问题示意图

研究内容

（1）合作博弈与非合作博弈框架

本研究的出发点是为了解决多主体城市边界控制问题中的非合作博弈问题，但此类研究目前缺乏足够的基准作为参考。因为相比于既有的基于CTM的城市边界控制研究，本研究在建模方式与求解方法上都进行了创新。为此，研究引入了一个中间场景作为间接对比，即合作博弈。合作博弈保留了集中控制范式的设定，假设存在一个中央管理者，能够控制区域路网中所有的道路交通流量。合作博弈可以被建模为一个MILP问题，为求解提供理论上的上限。同时，合作博弈也可以使用本研究提出的MARL算法进行求解。因此，通过合作博弈可以验证MARL求解算法的有效性。更进一步，在验证了MARL算法的有效性之后，可以通过对比研究合作博弈与非合作博弈，来探究两种博弈场景设定下的均衡状态差异。

（2）马尔科夫决策过程与贝尔曼方程

合作博弈与非合作博弈的目标在于寻找构成纳什均衡（Nash Equilibrium，NE）的策略集合，即在该集合中，没有智能体愿意单方面改变其当前策略。然而，直接求解大规模多主体博弈问题并找到任意一个NE策略集合通常并非易事，甚至在大多数情况下是不可行的。一个有效的方法是将寻找纳什不动点的问题转化为求解每个智能体对应的贝尔曼方程（Bellman Equation）。

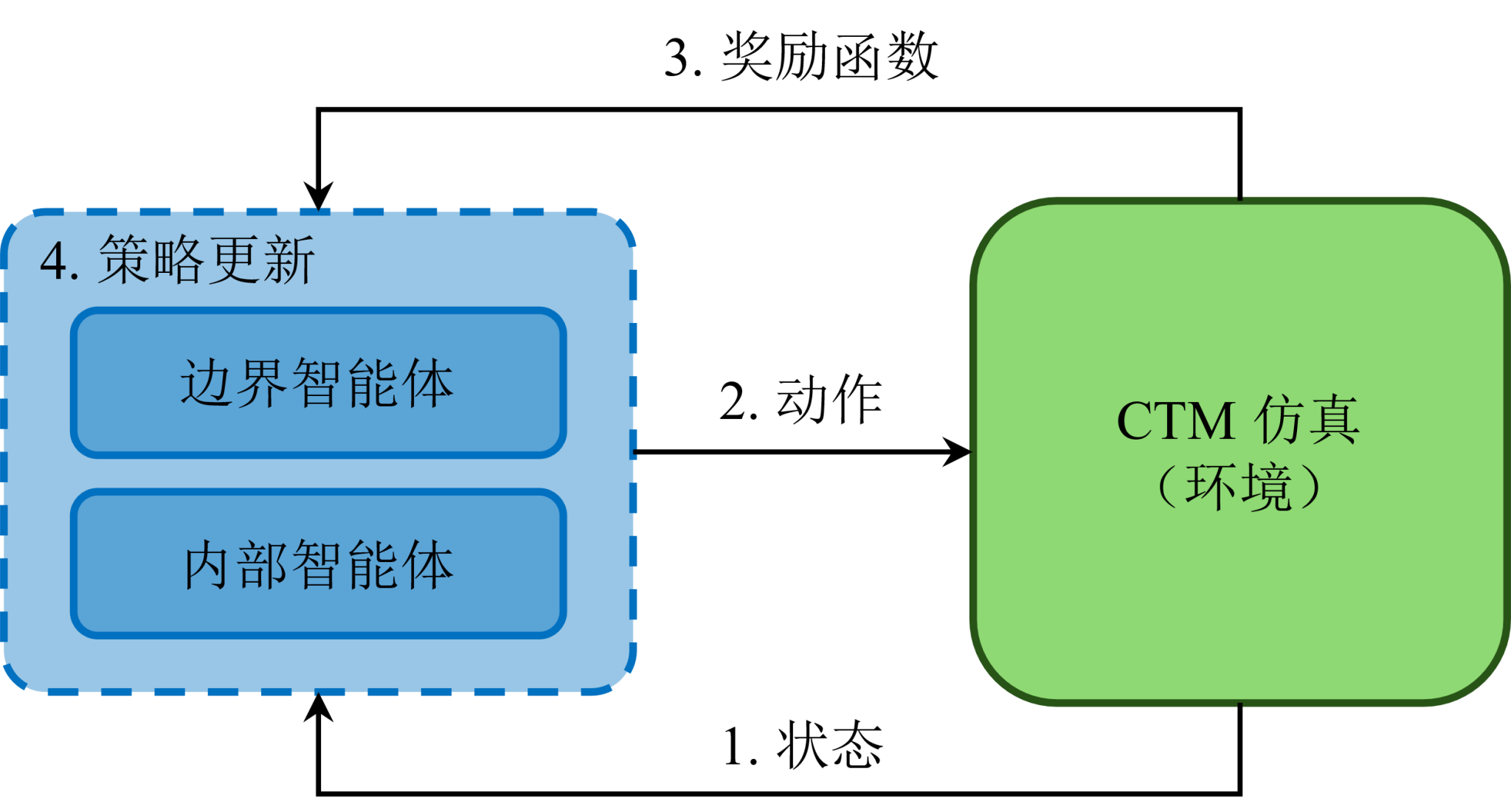
分布协调式边界控制问题强化学习示意图

（3）扩展平均场强化学习算法

本研究在基于CTM的城市边界控制问题中引入了MFD的概念，这一概念可视为平均场论中平均动作概念的雏形。基于此，我们提出了扩展平均场强化学习（Extended Mean-Field Reinforcement Learning，简称EMFRL）方法。进一步，研究提供了详尽的理论证明，证实了EMFRL算法在近似性与收敛性方面的理论完备性。结论显示，当智能体采用EMFRL算子进行策略更新时，能够收敛至一个稳定的策略。然而，这个策略与纳什策略之间存在一定的近似误差，但不存在收敛误差。此近似误差主要源于智能体自身策略与近似的平均场策略之间的偏差，并且随着智能体数量的增加，这一偏差将逐渐减小。

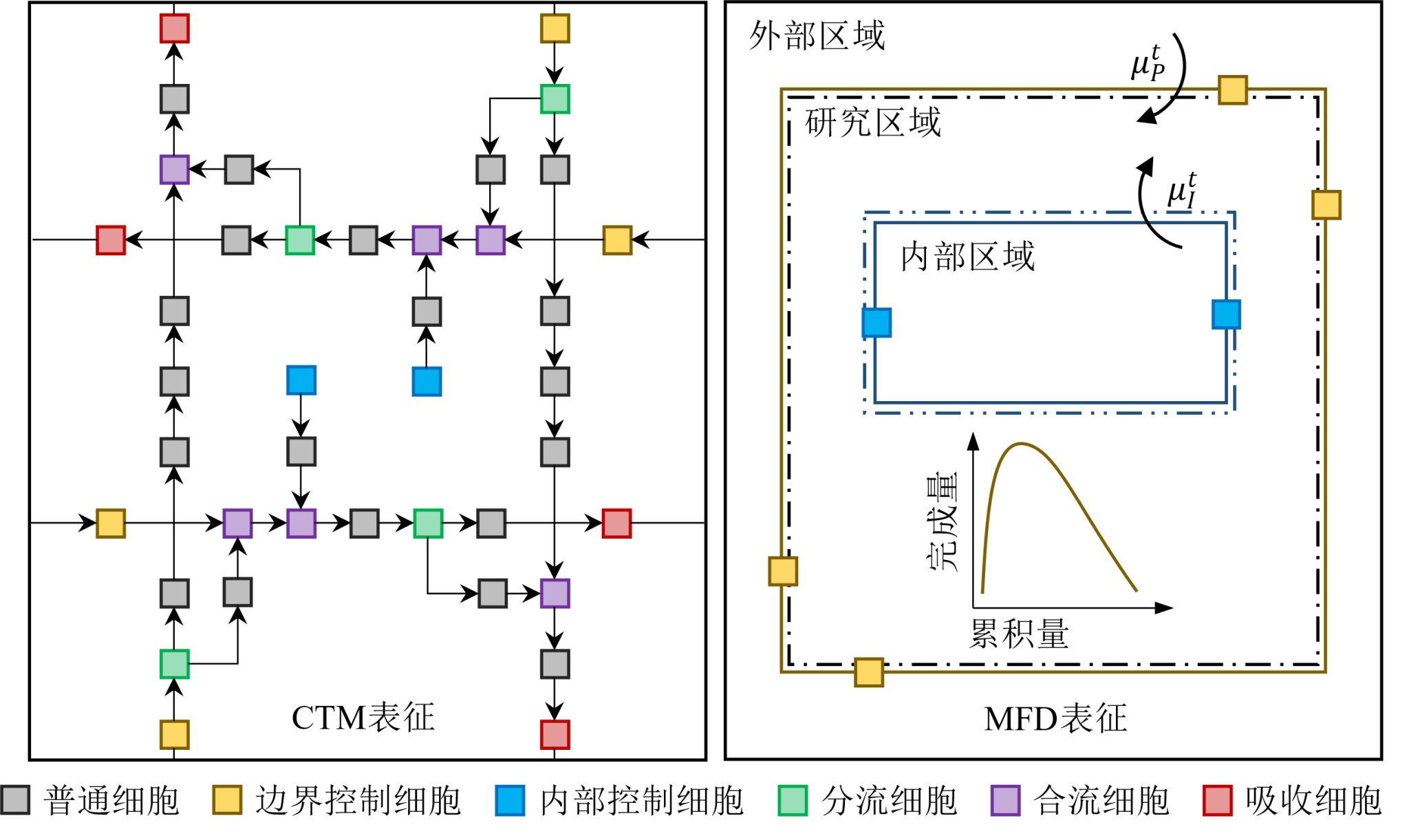
研究路网的CTM表征与MFD表征

（4）神经网络结构设计与置信分配

为尽量减少EMFRL中带有的近似误差。I）设计了本次实验中将采用的具体神经网络结构，通过在策略神经网络结构上增加了允许智能体突出特点的表达结构，增强了同一策略网络所能表达的复杂度并允许智能体学习到分化的子策略；II）引入了值分解网络（Value Decomposition Network，VDN）结构来增强同组智能体的特异性表达。

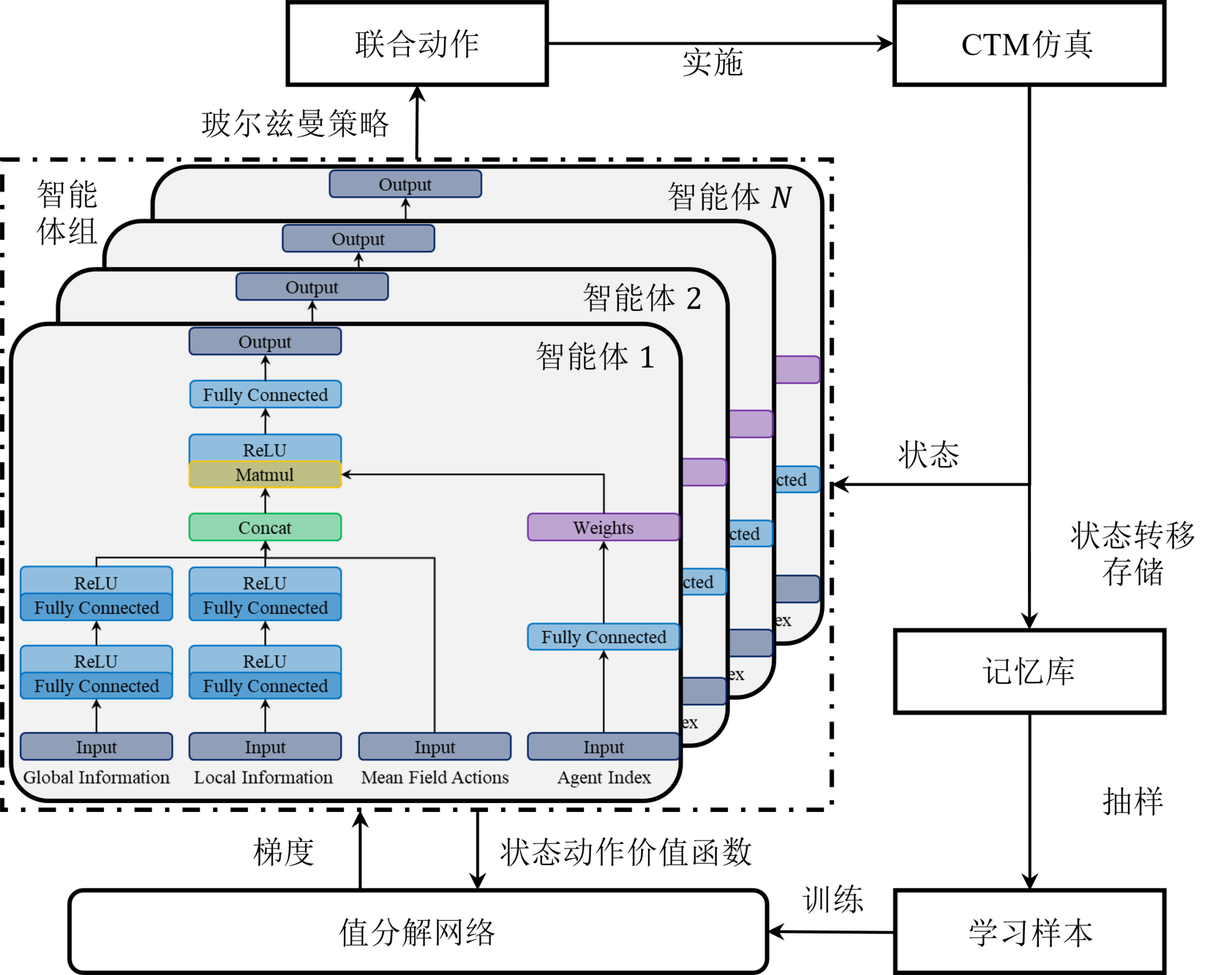
智能体神经网络结构及训练架构图

（5）平均场动作预测器

为解决平均场强化学习中的“鸡生蛋蛋生鸡”问题，研究提出了配套的平均场动作预测器（Mean-Field Action Predictor，MFAP）。MFAP以环境信息和上一个时刻的平均场动作作为输入，预测当前时刻的平均场动作。可以发现MFAP的训练问题属于机器学习中经典的监督回归预测问题。从直观上看，MFAP会随着智能体策略逐渐收敛到纳什策略的过程中也同步实现收敛。

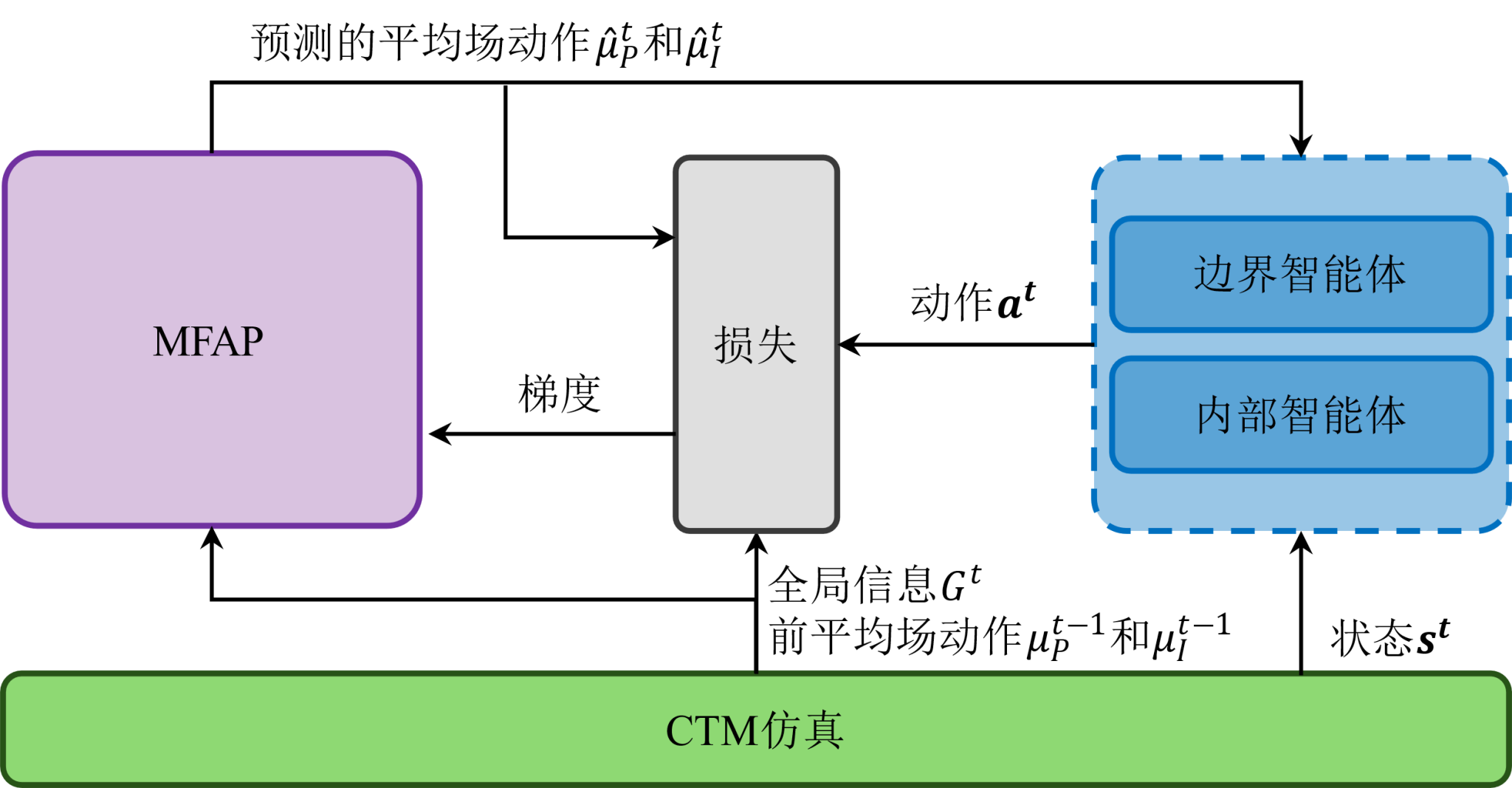
MFAP作用示意图

主要结论

以上海市徐汇区某地块路网为研究场景，占地面积约4平方公里。研究区域内含有25个信号交叉口，以及11个边界控制单元（边界信号交叉口）和3个内部控制单元（内部停车场）。研究将合作博弈和协调博弈的结果与不进行任何控制的基准策略进行了比较，同时，为了更加全面的描述EMFRL策略，列出了实验中将采用的各种边界控制策略及其各自的缩写。对于合作博弈（Cooperative Game，CP）来说，研究采用MILP模型（简记为LP-CP）、不进行任何控制（NM-CP）、MADDPG算法（MADDPG-CP）以及仅控制边界的MILP模型（PC-CP）作为对比，算法为采用MFAP的EMFRL（EMFRL-MFAP-CP）以及不采用MFAP的EMFRL（EMFRL-CP）。对于非合作博弈（Non-Cooperative Game，CD）来说，研究采用Bang-Bang控制（BB-CD）、MADDPG（MADDPG-CD）作为对比，算法为采用MFAP的EMFRL（EMFRL-MFAP-CD）以及不采用MFAP的EMFRL（EMFRL-CD）。

研究区域路网的CTM表达

（1）EMFRL的性能表现

以LP-CP策略为参考并以路网的总体表现为评价指标，可以得出研究所设计出的控制策略，EMFRL-MFAP-CP，EMFRL-CP，EMFRL-MFAP-CD以及EMFRL-CD分别可以达到LP-CP策略100.46%，99.91%，99.90%以及98.73%的性能。作为对比，其他边界控制策略，NM-CP，BB-CD，PC-CP，MADDPG-CP以及MADDPG-CD的性能表现就相对较差，只能达到LP-CP策略58.75%，74.26%，97.59%，81.54%以及88.78%的性能。

首先，EMFRL策略是一种可以带来正向收益的控制策略，相比与完全不进行任何控制的NM-PC策略，EMFRL策略可以在提高路网出行完成量以及降低内部排队两方面同时实现收益；其次，EMFRL策略在表现上接近由LP-CP策略所框定的理论上界。在实际到达的交通流量小于预期的场景中（叠加-30%到0%流量），LP-CP策略的表现效果要优于EMFRL策略，而在交通流量超过预期的场景中（叠加0%到30%流量），EMFRL策略的效果则反过来要更优于LP-CP策略。这主要是因为LP-CP策略难以对实际场景进行闭环控制，这在一定程度上也印证在面向类似于城市边界控制类动态问题时，采用在线控制范式的必要性；最后，通过EMFRL-MFAP-CP以及EMFRL-MFAP-CD策略之间的对比也可以说明，即便采用分布离散的控制模式，存在不同的控制目标，同时也缺乏直接的沟通联系措施，仅依靠路网反应出来的边界流率（平均场动作）和合适的协调机制（EFMRL-MFAP-CD），依旧不会影响路网在整体层面的表现。同时，这个结果也侧面印证了在引出平均场论中的一个假设：即采用基于CTM的城市边界控制问题的智能体仅需要边界流率就可以做出理想决策。

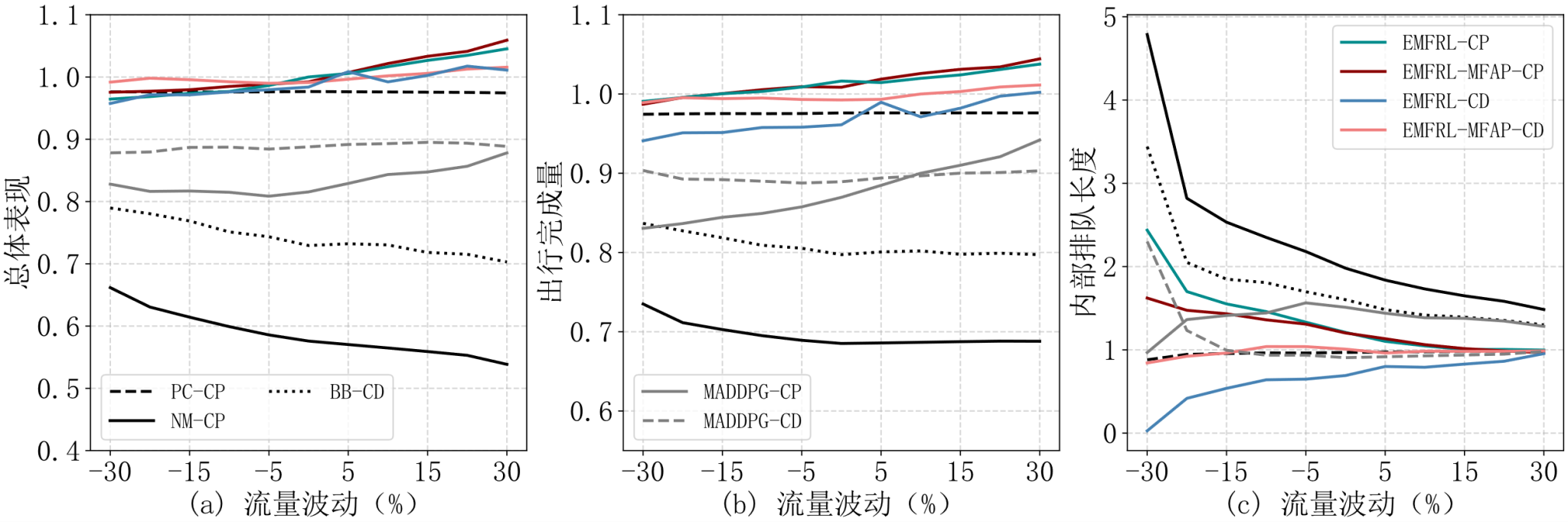
多种边界控制策略的性能对比

（2）合作博弈与非合作博弈的NE比较

合作博弈场景下，城市交通管理者拥有路网中所有智能体的控制权，因此，可以使路网累积量更为贴近交通拥堵的临界。从子图（b）中可以看出，这三种策略都允许路网累积量略微超过理想累积量，然后再逐步减少，从而使得累积量曲线整体更加贴合理想累积量，从而追求更高的出行完成量。而EMFRL-MFAP-CD和EMFRL-CD策略则显得更为保守，绝大部分时间内都将路网累积量控制在理想值以下。从另一个方面也能说明这三种策略的相似性，在没有流量波动的情况下，从子图（e）中可以发现，EMFRL-MFAP-CP，EMFRL-CP策略和LP-CP策略所产生的边界流入量是高度重合的。

非合作博弈场景下，对应着EMFRL-MFAP-CD和EMFRL-CD策略。这两种策略最为明显的特点就是在路网中内部智能体的地位要明显高于边界智能体。从子图（e）（f）中可以发现，这一组策略的内部流入量要明显高于其他边界控制策略，而从边界流入的量则低于其他策略。与前文分析相同，这是因为边界智能体不得不谦让协调内部智能体的控制决策，在尽量提高路网出行完成量的同时又必须留有充足的路网累积量冗余来避免交通拥堵的产生。因此这两种控制策略下，路网累积量在绝大部分时间下都低于理想值。

多种边界控制策略具体决策过程