
同济大学博士后,副研究员,中国公路学会青年托举人才。主要从事智能交通系统应用、智慧基础设施性能监测及相关工程领域研究。
本文作者:刘成龙, 陶莎, 赵聪, 暨育雄, 杜豫川
PART0:引言
电子不停车收费(Electronic Toll Collection, ETC)是智能交通的重要服务功能。1959年诺贝尔经济学奖得主William Vickrey首次提出电子收费系统的概念,1986年挪威成为世界上第一个大范围推广ETC的国家。1996年我国引入ETC系统,逐步在全国多省市高速公路推广应用。截至2019年12月,我国ETC用户累计达到19223.44万。2019年我国交通运输部提出,取消省界收费站后要确保ETC使用率达到90%以上,以保证整个路网运行畅通。该政策进一步加快了ETC的普及,并带动了全国范围的高速公路收费站改造和ETC车道的大幅增加。
我国高速公路收费站通常为混合收费站,同时布设ETC车道和人工收费(Manual Toll Collection, MTC)车道,以满足ETC和MTC车辆的通行需求。收费车道的布设与区域路网流量以及ETC普及率密切相关,对高速公路通行效率至关重要。若ETC车辆比例较低但ETC车道数量过多,会导致MTC车道拥堵,降低了收费站的整体服务能力;反之,若ETC车辆比例较高但ETC车道数量不足,则会导致部分ETC车辆转入MTC车道,使得ETC收费效率优势难以发挥。
面向单一高速收费站,现有研究主要集中在ETC收费站的交通流特征分析、收费站用户车道选择行为以及收费站布局优化设计三个方面。
在交通流特征分析上,Burris和Hildebrand采用交通仿真方法,量化分析了ETC车道对交通流的影响。Zarrilo等人提出了ETC车道的车辆队列长度与延误计算方法。刘伟铭等人针对ETC车道,建立了基于神经网络的当量通行能力估计模型以及服务水平分级模型,以评估收费站局部交通特性。Komoda利用智能体仿真建立了混合收费站的流量密度宏观基本图,刻画了收费站交通状态的动态演变。
在车道选择行为方面,Holguin-veras等人利用实测数据量化了支付费用、收费时间等因素对于ETC车道选择的影响。Saad利用驾驶模拟器分析了不同的收费站布局、标识牌类型以及可变信息版信息等因素对用户在收费站交通行为的影响,研究发现可变信息板可减少在收费口突然变道的行为。Xing等人考虑ETC和MTC共存的场景,综合分析用户在收费站换道行为产生的安全影响。
在单收费站布局优化方面,Bains等人利用VISSIM模拟了不同类型收费站的微观交通状态,并对收费站进行优化设计。罗梓铭等人利用排队论和交通仿真方法,分析了不同ETC普及率下收费站结构的适应性。马二顺在分析混合收费站交通流特性的基础上,提出了ETC车道物理尺寸的设计方法。Kim考虑了排队时间对于交通需求的弹性作用,提出了基于非线性优化与排队论的ETC车道布设方法。由于路网车辆路径选择与各收费站通行效率的交互影响,仅针对单收费站进行车道布设优化难以应对流量的动态变化,不能切实发挥路网各收费站ETC车道的效能。
面向路网层面多收费站的场景,现有文献主要针对收费站仅有ETC车道的情况,在考虑收费排队对车辆路径选择影响的基础上,研究车道布设数量及收费策略等问题。例如,Chen等人提出了基于马尔科夫决策链和随机用户均衡模型的收费站车道数量设置方法,及ETC收费策略。Borndorfer等人从博弈论的角度探析了ETC收费过程对路网交通流量分配的影响。Brotcorne等人采用双层优化模型设计了面向货运通道的ETC收费站布局方案。Chen等人以降低路网整体通行时间为目标,在路网的均衡分配模型中考虑收费站的特性。此外,Sharon等人针对自动驾驶车辆,利用多主体流程优化模型设计了一种基于路径的实时收费方法。鲜有文献根据混合收费站的特点,考虑不同类型收费车道布设、车辆路径以及收费车道选择的交互影响,在路网层面研究收费站的车道布设问题。
现有混合收费站的研究主要集中在通行能力预估与局部交通状态解析方面。如利用实测数据、微观仿真、现场试验等方法预估不同ETC与MTC车道比例情况下收费站的综合通行能力。Pokharkar等人基于实测数据分析了混合收费站的交通拥堵产生与疏散过程。Wang等人模拟了不同的混合收费站布设形态对车辆汇流特征的影响。这些研究虽然考虑了ETC与MTC车辆在收费站车道使用的权限差异,但未从宏观角度考虑其对路网交通流产生的影响,因而难以有效指导路网层面的ETC车道布设优化。
综上所述,现有ETC车道布设优化研究主要针对单收费站,或在路网层面考虑仅有ETC车道的场景,缺少路网层面混合收费站的车道布设分析和优化。不同类型车辆在不同收费车道的通行权差异会直接影响用户的路径选择与路网流量分配。
本文面向混合ETC和MTC车道布设的实际场景,从路网用户均衡的角度优化收费站车道布设方案。研究基于多类型用户路网均衡模型和排队论方法,建立基于双层规划的高速路网收费站车道布设策略。上层模型以车辆总通行时间最小为目标,优化设置进出收费站的ETC车道数量;下层模型为多用户路网均衡模型,有效反映ETC和MTC车辆的路径和收费车道选择行为。根据上述模型非凸非凹非线性的特点,设计了基于主动集(Active set)的启发式算法,解决了算法迭代过程中下降方向难以确定的问题。最后,以上海绕城高速路为例,评价验证模型的优化效果与适应性。研究成果可为我国收费站车道布设方案的设计提供可靠的理论方法支持。
PART1:模型构建
在混合收费站,ETC车辆可使用ETC与MTC车道,而MTC车辆仅能使用MTC车道。为表征混合收费站的车道使用规则及ETC车辆的收费车道选择行为,提出了一种混合收费站的等价拓扑结构,如图1所示。图1(a)的路网中,节点A,B,C,D 为收费站,A和B为入口收费站,C和D为出口收费站,收费站均设置ETC与MTC车道。图1(b)将收费站节点转化为ETC和MTC分离的节点。图1(c)为等价的网络拓扑结构,其中N1-N7(路段由其起终点与直线连接符命名,其中N1表示起点为节点1,N7表示终点为节点7)、N11-N2、N2-N4等为实际路段,N7-N15、N7-N16等为虚拟收费路段,N15-N11、N16-N11等为虚拟连接路段。
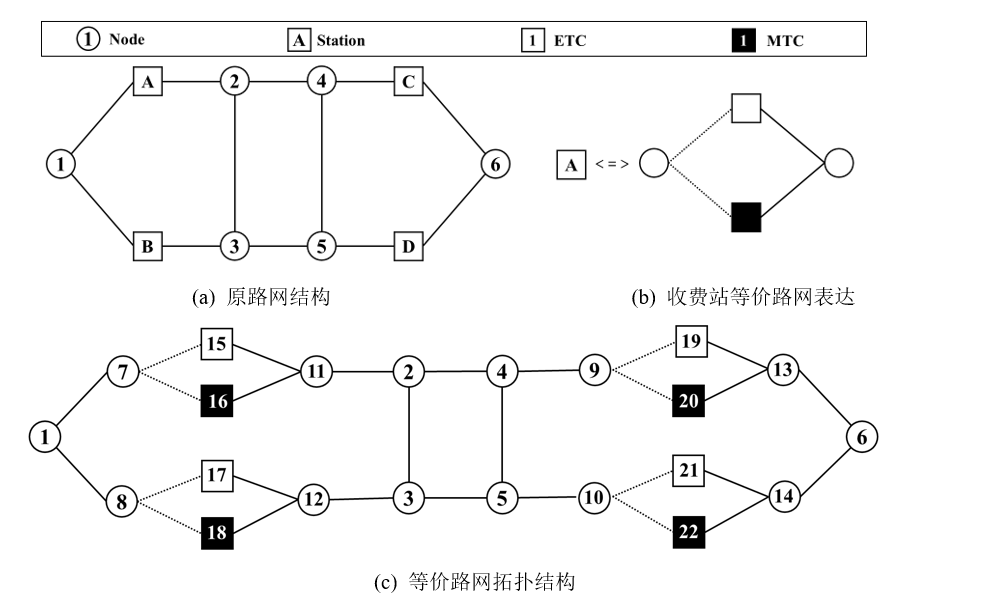
图1. 面向混合收费站的等价网络拓扑结构
等价路网包含实际路段、虚拟收费路段和虚拟连接路段。为准确预估车辆在路网中的路径选择,分别建立三类路段的费用函数。为表示通行时间、排队时间对用户选择的影响,并与用户均衡模型相适应,路阻函数须具有明确的数据表达并可以从宏观流量角度描述其对路段的影响,故实际路段的费用采用BPR函数计算,虚拟连接路段的费用设置为0,如式(6)所示。考虑M/M/N在双层迭代中会产生巨大的计算压力,且本文主要将ETC和MTC分别视作同一化的两种收费口,因此采用M/M/1排队论模型计算其排队时间,如式(7)-(8)所示。
面向混合收费站的路网用户均衡模型(User Equilibrium, UE)可表示为式(9)-(12),其描述了路网层面混合收费站不同的收费车道布设方案,ETC和MTC车辆的路径选择以及ETC车辆的收费车道选择。式(9)为多用户均衡的目标函数;式(10)表示每类车辆在路径上的流量和等于给定的交通需求;式(11)保证了流量的非负性;式(2)表示路径流量与路段流量的关系。
收费车道布设问题可表征为管理人员与用户的博弈过程。公路管理者通过调整收费车道的布设,影响车辆的出行选择;车辆的出行选择会影响路网和收费站的通行效率,从而影响管理者的决策,如图2所示。图2(a)表示初始收费车道布设条件下车辆的分布情况,收费站A和C有5条ETC车道和1条MTC车道,B和D站有1条ETC车道和5条MTC车道。大多数ETC用户会选择路径①,利用ETC车道快速通行;而大多数MTC车辆会选择路径②,以避免收费站A与C过长的收费排队。选择收费站B的ETC车辆甚至可能转移到MTC车道行驶。图2(b)为调整后的方案,部分MTC车道在收费站B转换为ETC车道,同时部分ETC车道在收费站A转换为MTC车道。方案调整后,部分的MTC车辆会转移到路径①,且部分的ETC车辆会转移到路径②。

图2. 收费车道布设对用户路径选择的影响
本文采用双层规划模型表征管理人员与车辆的博弈过程,模型假设如下:
(1)路网的车辆的起讫点需求(Origin-Destination, OD)与ETC普及率已知,不随车道布设方案变化;
(2)路网各收费站的总收费车道给定;
(3)ETC与MTC车辆对于收费排队时间和路段通行时间的感知无差异;
(4)当ETC车道的流量超过服务能力,ETC车辆会主动转至MTC车道通行。
高速公路收费车道优化布设双层规划模型可表示为式(1)-(12):

式(2)保证了当ETC普及率未到100%,收费站至少预留1条MTC车道,式(3)为总收费口数量约束,式(4)为非负性约束,式(5)表示上层的流量由下层优化求解。由于下层目标函数(9)不是严格凸函数,实际路段上两类用户流量解不唯一,但路段总流量解唯一。路网拓扑结构中将ETC与MTC车道进行了分离,式(9)中足够大的惩罚数B保证了ETC车道上MTC车流量为0。两类车辆路段流量解不唯一不影响收费车道服务时间的计算。
PART2:基于主动集的求解算法
针对研究问题的特殊性,上层模型变量(ETC车道数量)为非负整数,且受到收费站总车道数量约束,下层模型为非凸非凹非线性的多类用户均衡函数,很难直接求解全局最优结果。因此本文设计了基于主动集法(Active set) 的求解算法。
主动集法将初始提供的可行解不断迭代优化,寻找其最佳梯度下降方向,直至结果收敛。该方法可分别处理上层和下层模型,不必在每次迭代中考虑上下层之间的参数交互。由于双层规划模型难以直接求解下降梯度的最佳步长,因此将模型变量ETC车道数量转化为二进制,这样自变量就可以变为0和1的两个主动集合,而模型的优化过程也变为两个集合之间的元素交换,这样就可以将下降步长锁定为1,从而仅需确定下降方向即可。
主动集法首先确定一组可行解,在之后的迭代过程中,每一次都会在0集合和1集合之间交换元素,降低目标函数值。而元素交换的方式就是选取模型的最佳下降方向。由于Karush-Kuhn-Tucker (KKT)条件是非线性优化问题最优解的必要条件,其利用拉格朗日乘子法从等式约束扩展至不等式,因此,选择交换的元素序号可通过拉格朗日乘子的情况进行估算。
0集合和1集合所对应的乘子在经济学中也被称为影子价格,表示放宽约束后产生的边际效用,或者加强约束产生的边际成本。假设现有一组模型初始可行解,为了寻找一组更优的可行解,需尽可能降低拉格朗日函数的值。因此,对于某些原属于0集合的元素,如果其拉格朗日乘子小于0,则将其移动至1集合中,反之,对于原属于1集合的元素,如果其拉格朗日乘子大于0,则将其移动至0集合中,从而降低拉格朗日函数目标值。
虽然迭代过程可以降低目标函数(1)的值,但在进行0集合与1集合的元素交换时,可能违背二进制约束,且由于未控制模型对应的拉格朗日乘子,二进制变量的乘子仅能近似表示目标函数变化。为了保证每次迭代过程中目标函数(1)下降,以防止迭代循环,并使二进制在过程中始终生效,式(13)-(17)作为内嵌的优化函数加入循环中,从而获得可行的较优解。

在计算过程中,在给定的一组初始可行解下,利用Frank&Wolfe法直接求解下层的UE问题,获得该条件下的路网流量。在已知流量的条件下,利用上层函数的边界变化求解拉格朗日乘子对,最终求解内嵌优化模型(13)-(17),将可行解从0,1集合中进行调换,从而获得更优的可行解。重复上述迭代过程,直至目标函数(13)为0,则无更优的解可以迭代产生,从而获得模型最优解。

图3. 主动集法求解流程
PART3:实例分析
选取上海市绕城高速作为研究对象,图4为简化后的绕城高速内主要路网,其中A~F代表6个主要收费站,每个收费站分为上、下匝道两个方向,区域1~5代表考虑的主要OD区域。表1为各区域间的OD数据,本文仅考虑通过绕城高速的车辆需求。高速全段为双向八车道,单车道通行能力设为1500 pcu/h,城市道路单车道通行能力设为800 pcu/h。A~F各收费站单向收费车道总数为7条,ETC车道服务能力为1500pcu/h,MTC车道服务能力为800pcu/h。
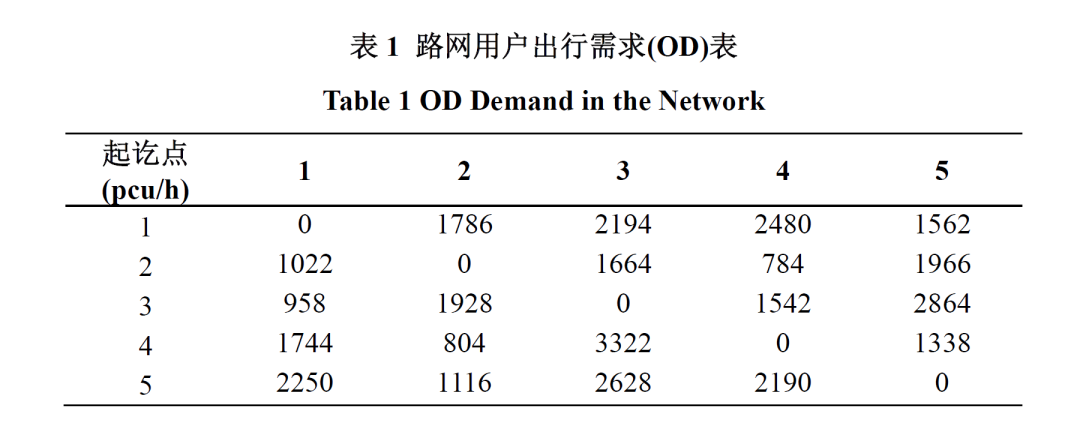
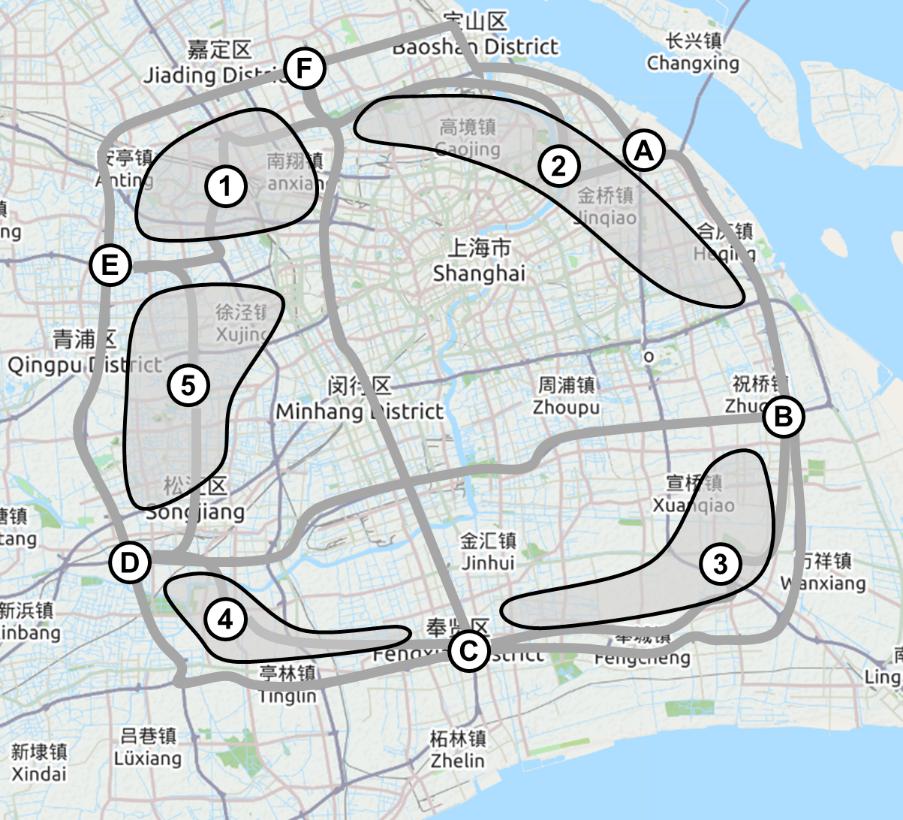
图4. 上海市绕城高速示例区域
图5为实例的网络拓扑结构。在等价的拓扑结构中,蓝色节点代表收费车道与实际道路的连接处,分别代表6个收费站,红色位置为用户OD矩阵的虚拟中心。绿色与红色箭头代表单向收费路段,黑色路段为实际道路,均为双向道路。经转化后路网变为含有71个节点,共120个路段。
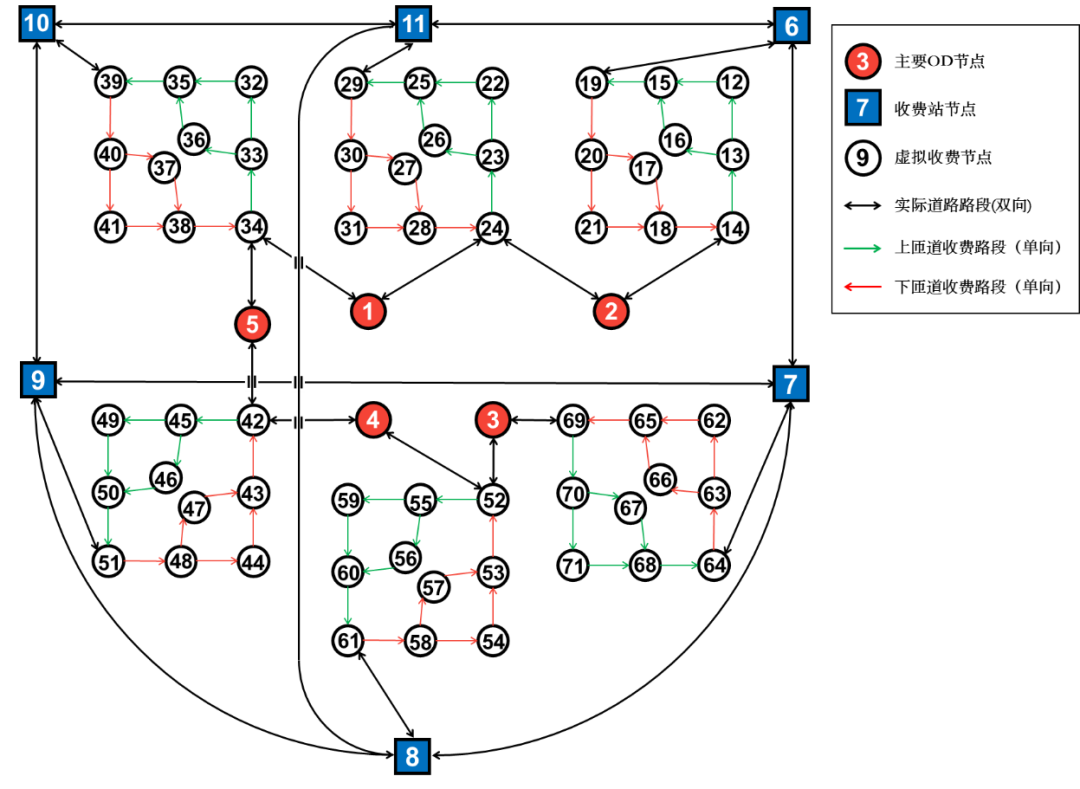
图5. 示例网络等价拓扑结构
设置从0%至100%的ETC普及率,对六个收费站的ETC车道数量进行优化,优化结果如表2所示。为保障MTC车辆的通行权,如ETC普及率低于100%,各收费站至少设置一个MTC车道。随着ETC普及率的提升,各收费站的ETC车道数量一般随之上升,带来收费排队时间的下降。当ETC普及率从20%增加到30%,A区进口ETC车道减少一条。其原因在于,区域2有A和F两个上下高速公路的收费站,减少A收费站的ETC车道可驱动ETC车辆至F收费站,F收费站的ETC收费车道数量足够满足ETC车辆需求,增加A收费站的MTC车道可降低MTC车辆的通行排队时间。
当ETC普及率从0%提高至100%,收费排队时间呈负指数下降,共降低了95.16%。当ETC普及率较低时(≤20%),提升ETC普及率带来的效益明显,普及率提升10%,收费排队时间平均下降52.4%,少量的ETC车道即可发挥10%的ETC车辆的快速缴费优势,边际收益明显。当ETC普及率超过20%,其产生的排队时间下降率逐渐减小,提升ETC普及率10%平均降低收费排队时间12.15%,如图6(a)所示。当ETC普及率达到90%时,ETC车道数量明显上升,表明仅保留少数基本的MTC车道即可保证非ETC车辆的稳定通行,而充分发挥了ETC车道的通行效率优势。当ETC车辆的普及率达到100%时,则无需在各收费站设立MTC车道,从而实现了100%的ETC收费站应用率。
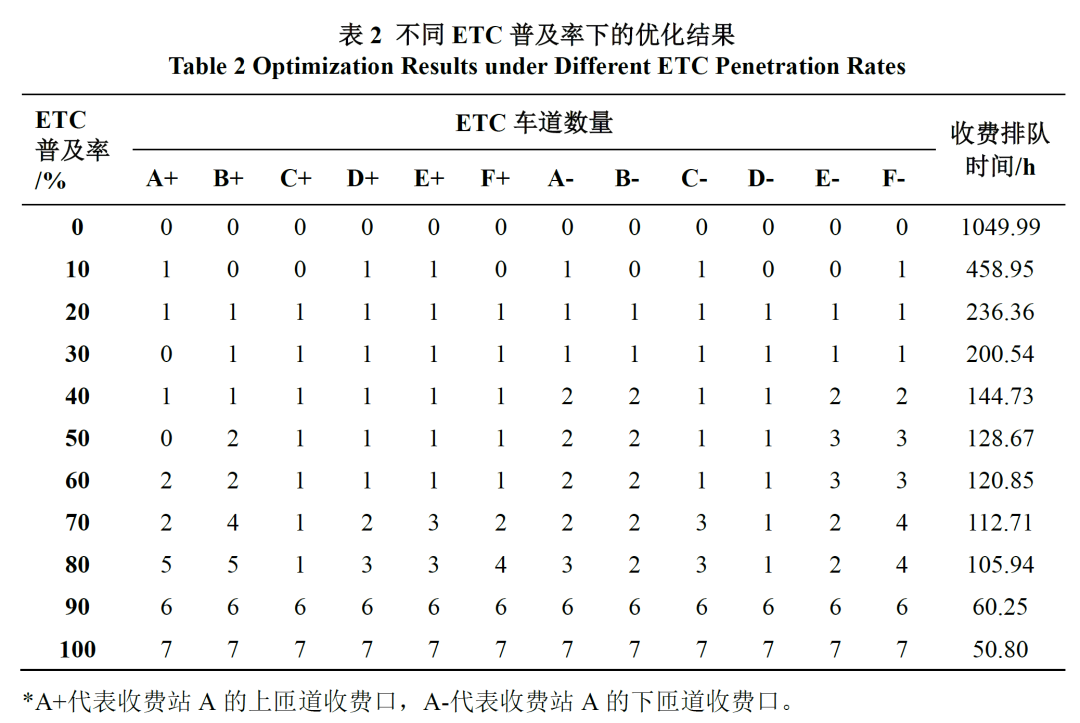
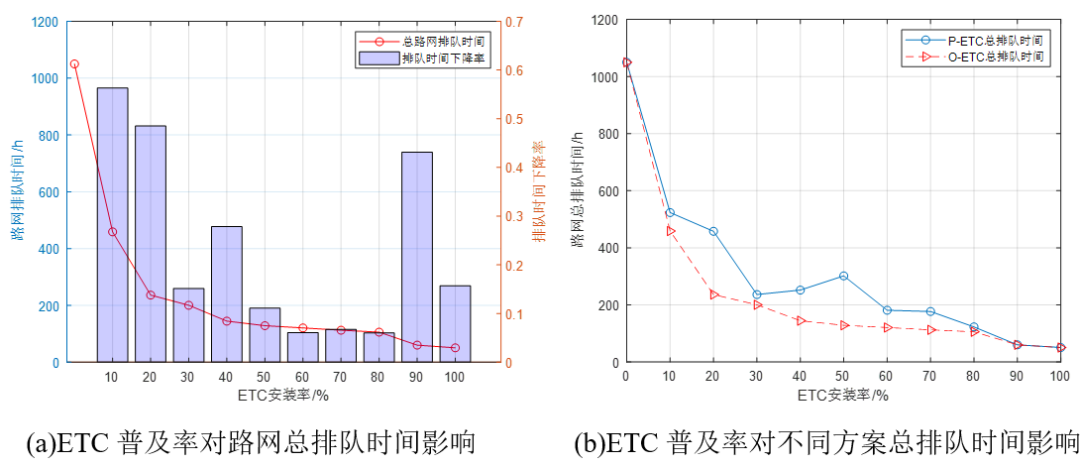
图6. ETC普及率对ETC车道布设方案影响
表3比较了本文提出的ETC车道优化布设法与比例布设法的结果。其中P_ETC依照各收费站ETC车辆比例配置ETC车道数量。O_ETC代表本文提出的双层模型优化结果。由于未考虑不同收费站之间的交互影响,比例布设法可能导致部分收费站MTC车道拥堵,产生较高的收费排队时间。而本文提出的O_ETC方法则根据路网的OD与设施情况调整ETC车道的路网分布情况,在保证通行效率的同时,降低ETC的改造数量与成本。相比于P_ETC布设,本文提出的优化方法可降低0.08%~57.37%的收费排队时间,通行效率提升效果显著,尤其在ETC普及过程中(10%~70%),O_ETC的优势可以充分发挥,如图6(b)所示。当ETC普及率从30%升至50%,比例布设法可能导致收费排队时间增加。其原因在于,过多的ETC车道压缩了MTC车道数量,导致MTC车道的排队时间加长。当ETC普及率超过90%时,两种布设方案取得的效果基本一致。
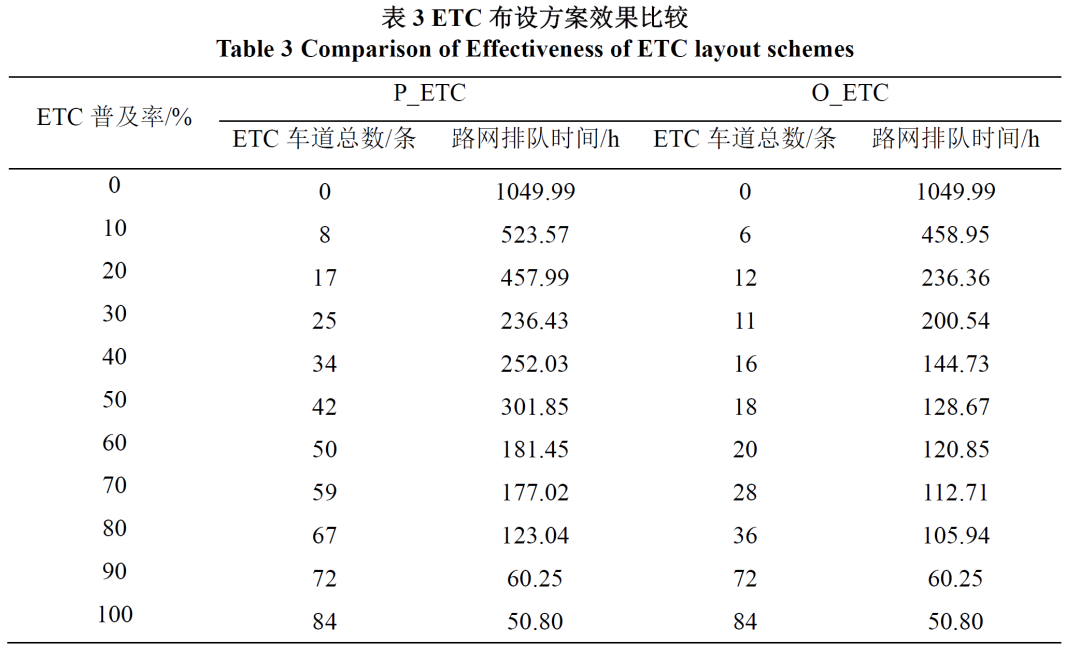
通过实例分析可以看出,本文提出的基于双层规划的ETC车道布设方案可以有效降低路网整体通行时间,尤其在ETC普及前期阶段,过多或过少的布设ETC车道都会影响整个路网的通行能力。相较于路网多节点ETC车道平均布设的方法,本文提出的优化模型不仅可以降低ETC的建造成本,同时可以降低总体的排队时长。
基于双层规划的路网不停车收费车道优化方法适用于路网中同时存在多个收费站节点,且OD间可行路径不唯一的情形。因此,可应用于城市高架路网、小规模区域高速路网等场景。当路网节点数量较多,车辆行驶路径中需通过多个收费节点时,等价路网结构较为复杂,应首先筛选出与起讫点唯一对应的收费站(即达到/离开用户起终节点必然经过的收费站,一般为城市的入口/出口),从而对其拓扑进行简化,降低模型的计算压力。
PART4:结语
(1)本文根据高速公路混合收费站的特点,设计了混合收费站的等价拓扑结构,表征混合收费站的车道使用规则及车辆的收费车道选择行为;结合多用户路网均衡模型和排队论方法,建立了多用户路网均衡模型;在此基础上,提出了基于双层规划模型的高速公路ETC车道优化布设方法,描述了收费车道布设与车辆出行路径选择及收费车道选择的交互作用,考虑了车道布设对ETC和MTC车辆的不同影响。
(2)根据模型的特点,设计了基于主动集的启发式算法,利用参数二进制与拉格朗日函数法确定迭代下降方向,避免了下降步长难以计算的问题;通过内嵌优化函数的方式,避免了主动集转化过程中约束失效的问题。
(3)以上海市绕城高速为案例,比较分析了不同ETC普及率下收费车道布设方案及其效果。当ETC普及率从0%提高至100%时,收费排队时长呈负指数趋势下降,共降低95.2%。与比例布设法相比,本文提出的方法最高可降低57.4%的收费排队时间。
(4)从路网宏观角度提出的ETC车道布设优化方法,可以在保证通行效率的同时,有效优化不同节点的ETC建设方案,避免过多或过少的ETC车道对路网运行造成的负面影响。
(5)本文提出的等价拓扑结构将1个收费站节点扩充至12个虚拟节点,加大了模型的计算量,使其在大范围的路网应用产生巨大的计算压力。此外,本文虽然在收费车道布设中考虑了收费车道的车辆排队,但未考虑收费车道排队溢出对其他收费车道的影响。因此,未来研究主要侧重在量化排队溢出的影响,进一步简化模型的网络结构设计,讨论不同的收费模型对于优化结果产生的影响。